Dale Andreatta, April 30, 2003

Background and overview

Recently, success has been achieved in making insulative bricks for stoves. My work here seeks to answer the following questions:

1. What are the thermal properties of these bricks? The properties of interest are density, specific heat, and thermal conductivity.
2. Is it possible to estimate how much heat will be lost from a stove? Is it possible to reduce this to a simple formula that could be evaluated using a calculator? Alternatively, could one express this heat loss on a graph or series of graphs?
3. How do the measured properties influence the overall heat loss from the stove? How insulative is insulative enough, so that overall heat loss is minimal?
4. Is there a correlation between one property and the others, such that one property (density for example) could be easily measured and the heat loss from the stove quickly estimated?

Results-General

The 6 samples supplied by Dean Still and Damon Ogle were:

1. Guatamalan baldosa
2. A 50/50 mix of sawdust and clay
3. A mix of 85% vermiculite with 15% clay fired at unknown temperature.
4. A mix of 85% pearlite with 15% clay fired at unknown temperature.
5. El Coco baldosa made from clay, volcanic ash, and horse manure (no jokes please). Firing temperature was 950 C.
6. Pumice brick (A brick of 2420 cc of pumice aggregate, 360 cc clay, 750 cc water, fired to 950 C in the brick kiln near El Coco.)

The results are given in the table below, and the properties of “ordinary brick” and glass wool are also included and are taken from a heat transfer textbook (Ref. 1, Appendix D). Glass wool might be considered the best possible insulation.

In the table below, the measured properties are given, along with the heat loss of a stove with walls made of a material with these properties. Appendix 1 contains details of the measurement methods, and Appendix 2 contains details of the heat transfer calculations, though Appendix 2 is more for the technical reader.

Table 1: Summary of measured material properties, and calculated heat loss.

In the right column the assumptions are that the stove has an internal area of 0.1178 m^2 (corresponding to a tube 0.3 m tall and 0.125 m in diameter or 12 inches by 5 inches in English units) that the inside gas temperature is 700 degrees C higher than the ambient temperature, that the wall thickness is 3 cm, and that the cooking event lasts 1 hour. If one increases the inside surface area of the stove by x%, the total heat loss will increase by the same factor. If one increases the gas temperature above the environment by x%, the total heat loss will increase by the same factor. Other variables are not as easy to translate.

All measurements of conductivity were done at room temperature, while the bricks would be used at somewhat higher temperatures. It appears that the conductivity of solid bricks stays roughly constant as the temperature varies, while porous or lightweight bricks have a conductivity which goes up as the temperature increases. Limited data suggests that the conductivity roughly doubles as the temperature goes from ambient to 2300 F (1260 C). This variation in conductivity was built into the numerical model described in Appendix 2. The results show that for the porous ceramics, the heat loss increases by about 10% due to this increase in thermal conductivity. The results in Table 1 assume a constant thermal conductivity, so one might add about 10% for materials with densities less than 1000 kg/m^3.

The heat lost from the gases goes to 2 places. A portion of the heat goes into the stove body and is retained in the body. Another portion goes into the stove body but then passes through and into the environment. For the lightweight materials, the amounts of heat going into the 2 places are generally about equal. For the heavier materials (baldosa) a larger proportion is retained in the stove body.

It turns out that the thickness of the stove wall is relatively unimportant in determining the total heat loss. As the stove wall gets thicker a greater amount of heat is retained in the stove body, but a lesser amount passes through the stove wall. As the wall thickness decreases below about 2 cm, the loss increases rapidly, but increasing the thickness much beyond 3 cm has little effect. Very thick walls actually loose more heat since so much heat goes into the body. The optimum thickness is generally around 5 cm, but there is usually a broad band in which heat loss is near minimum. The 3 cm used in these calculations is a compromise. The detailed heat transfer calculations described in Appendix 2 could be used to find an optimum thickness, but for most materials this is about 5 cm, and the heat loss isn’t much less than at 3 cm.

I believe that, as a rule of thumb, a heat loss of 1 MJ is about as low as we need to go. This would correspond to about 56 grams of dry wood. This is only a small percentage of the heat being released, perhaps around 5%. Lowering the heat loss further would not give substantially better cookstoves. We can see in the above chart that several materials currently available get heat loss close to about 1 MJ. Hence, future work might be directed at increasing their longevity if necessary rather than improving their thermal properties much further.

Correlation of properties

In question #4 posed in the introduction of this report, I threw out the idea of finding some correlation between an easily measured property (such as density) and all of the thermal properties, such that one could measure the density and simply consult a table or graph (like those contained in the following section) to find the approximate heat loss.

It appears that specific heat doesn’t vary much among the various stove materials. Among the range of all solid materials, specific heats vary by a range of about 5:1, compared to thermal conductivities which vary over a range of thousands. Among stove materials, specific heats vary by about 10% from a middle value. (This +/- 10% variation causes only about a +/- 2.8% variation in calculated heat loss.) I propose that in the future we should not bother measuring specific heat, and in our calculations we should do one of two things, either use a universal value for all stove materials (I propose 835 for this common value) or estimate a value for a specific material based on the information in the table supplied below. Values estimated from this table are probably about as accurate as I can measure them.

Table 2: Specific heat of common stove materials.

The conductivity doesn’t appear to have any universal correlation with density. Guatamalan baldosa is just as dense as an ordinary brick, but has only about 40% the conductivity. Of the 4 light-weight bricks tested, there is generally an inverse trend, the ones with the higher density have lower conductivity. Still, the light bricks had much lower conductivity than ordinary brick, and baldosa, so there is a general trend that lower density leads to lower conductivity.

A method of estimating heat loss over a variety of conditions

With regard to question #2 in the introduction, I believe there is no good simple formula for calculating the heat loss from a stove that is universally applicable, however it is possible to generate “maps” of heat loss factors from which one could quickly estimate the heat loss once density and thermal conductivity were known. Three such maps are given here. They are based on the same calculations as the results in Table 1. Use of the maps should give an answer that is nearly as accurate as the full calculations.

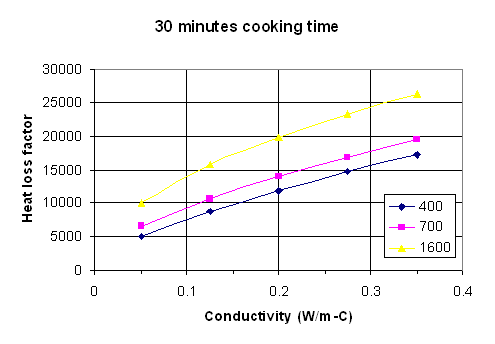
Fig. 1: Heat loss factor vs. thermal conductivity for 30 minutes cooking time with density as a parameter. Density units are kg/m^3.

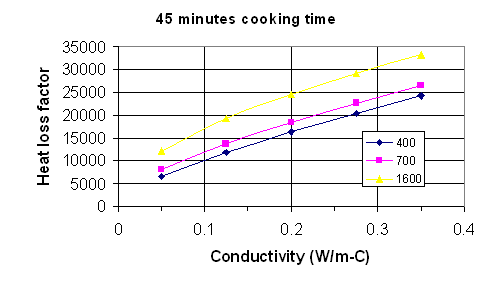
Fig. 2: Heat loss factor vs. thermal conductivity for 45 minutes cooking time with density as a parameter. Density units are kg/m^3.

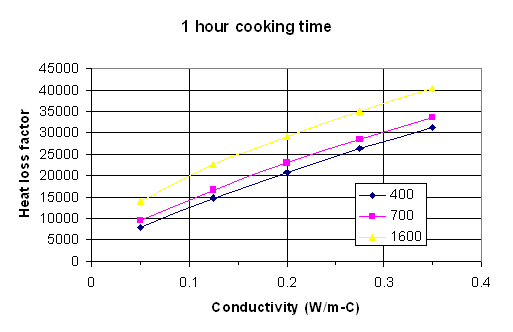
Fig. 3: Heat loss factor vs. thermal conductivity for 60 minutes cooking time with density as a parameter. Density units are kg/m^3.

To use the maps, the following procedure should be followed.

Measure or estimate the internal surface area of the stove in square meters. Measure or estimate the gas temperature exiting the stove, and subtract from this the ambient air temperature. Do this in degrees C. The heat loss from the stove will be the area times this temperature difference times the heat loss factor.

To estimate the heat loss factor, pick the graph that most closely corresponds to the cooking time. Measure or estimate the density and thermal conductivity of the stove material. Go along the horizontal axis to the value of thermal conductivity, then up to the appropriate curve for the density of interest. If the actual density is not one of the values for which there is a line, go between the lines at an appropriate height. Follow across horizontally from this point to the heat loss factor on the vertical axis.

If the cooking time is greater than 1 hour, do the above procedure for both 1 hour and ¾ hour. After 45 minutes the heat loss rate is essentially constant, so take the difference between the 1 hour heat loss factor and the ¾ hour heat loss factor, multiply this difference by the time after 1 hour in which you are interested, and add this to the 1 hour factor. For example, if the cooking time is 1 ¼ hours, take the 1 hour heat loss factor and add to it the difference between the 1 and ¾ hour heat loss factors. If the cooking time is 1 ½ hour, take the 1 hour factor and add to it twice the difference between the 1 hour and ¾ hour factors.

The product of the heat loss factor times the internal area times the temperature difference is the total heat loss in Joules. Divide by one million to get the heat loss in Megajoules (MJ).

Some notes on water absorption and toughness

Being porous, the samples tend to absorb water. This is probably not important in a working stove, but may be important if anyone wants to reevaluate these thermal properties in the future.

The absorption was not studied in detail, but it was found that 2.07 kg of dry Guatamalan baldosa picked up at least 0.57 kg of water, or 28% of its dry weight.

It was also noted that the pearlite and vermiculite mixes were both strong and tough, while the other samples were not. (In engineering terms “strong” means that it takes a lot of force to break a specimen, and “tough” means that it takes a lot of energy to break a specimen.) The pearlite and vermiculite had to be beaten hard with a hammer to break them, while the baldosa could be broken with light taps and the sawdust/clay could be broken by hand. Dents were observed in the tough samples when struck with a hammer.

Future work

Now that the testing methods have been developed and practiced, additional samples can be tested more quickly. I would be willing to occasionally test a sample.

References

1. Heat and Mass Transfer, Frank M. White, 1988, Addison Wesley Publishing Company.

2. Fundamentals of Heat Transfer, Frank P. Incropera and David P. DeWitt, John Wiley and Sons, 1981.

3. Marks’ Standard Handbook for Mechanical Engineers, Baumeister, Avallone, and Baumeister, 8th Edition, McGraw-Hill Book Company, 1978.

Appendix 1: Measurement of properties

Density was the easiest property to measure, and was probably measured the most accurately. The dimensions of the bricks were measured, the volume was calculated, and the brick was weighed on a scale. The density was calculated.

Specific heat was measured by breaking the brick up into small pieces, perhaps golf ball size. These pieces were put into an oven for a couple hours, so that the pieces were of uniform temperature, and the temperature was known fairly accurately by measuring the temperature of the oven with a thermocouple. The pieces were taken out of the oven and quickly transferred to an insulated container containing cool water. The water temperature had previously been measured. The insulated container was covered, and occasionally sloshed around. After a couple hours, when the bricks and water had achieved uniform temperature, the water was drained off, mixed, and its temperature was measured. The specific heat was calculated from the fact that the energy gained by the water was equal to the energy lost by the brick pieces. (The amount of water that was used was selected so that this final temperature was not too different from room temperature, so that not much heat would be transferred from the water to the room or in the opposite direction.)

Thermal conductivity was measured directly by building a stack containing a sample of the material to be measured and a piece of ¼ inch (actually 0.24 inch) Styrofoam with thermocouples measuring the temperatures at the top, bottom, and middle of this stack. See sketch below. The stack was placed on a heat sink of nearly constant temperature (a block of ice that was in the process of melting) and a heat source (a large pot made of steel that remained a nearly room temperature) was placed on top of the stack. The thermal conductivity of the sample can be related to the thermal conductivity of the Styrofoam from the relative magnitude of the temperature differences across the layers. A total of 3 thermocouples are used. Where the block shapes are somewhat irregular, copper wool was used to transfer heat more uniformly. Heat transfer should be essentially 1-dimensional at the center of the sample. Thermal conductivity of the Styrofoam (0.029 W/m-C) is known from its advertised R-value of R-10 in 2 inches. The thermocouple at the ice interface was nearly constant at a few degrees above the freezing point. The heat source temperature was nearly constant at just below room temperature. A time of about 2 hours was usually needed to stabilize temperature but before the ice started to melt excessively.

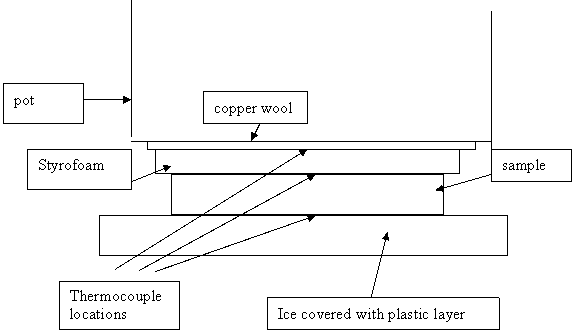
Fig. A1: Schematic drawing of apparatus used to measure thermal conductivity.

Appendix 2: Calculation of Heat Loss

A 1-dimensional 10-node finite difference model was used. This method works for both round and rectangular stoves when the stove wall is fairly thin compared to the width or diameter. The inside node temperature was assumed to be the same as the gas temperature. This assumption is probably the most questionable. Preliminary calculations were done using a convective boundary condition at the inside node. Boundary layer calculations show that the idealized convective heat transfer coefficient on the inside would be on the order of 10 W/m^2-C in the combustion zone, and about half this at the stove exit. However, there will be considerable turbulence from a number of sources increasing this value. Preliminary calculations show that increasing the heat transfer coefficient beyond about 20 led to little additional heat transfer in most cases, as the inside wall was close to the gas temperature anyway. Preliminary calculations show that radiation is very important in the combustion zone area but not important away from the combustion zone. The results of this model will probably significantly underestimate the heat loss in the combustion zone, but overestimate the heat loss somewhat from the non-combustion zone, generally averaging out.

The outside air temperature was assumed to be known and constant at about 20 degrees C, while the outside node lost heat by both radiation and convection with variable convective heat transfer coefficient. The initial temperature of the stove was assumed to be the ambient temperature. Constant material properties (both solids and fluids) were assumed. Convective heat loss was calculated using a Nusselt-Rayleigh number correlation from Ref. 1, p. 397. Radiation was calculated from the difference of the temperatures to the 4th power. Perfect emissivity was assumed. (As a rule of thumb, the radiative losses are about 3 times the convective losses.)

The total heat lost from the inside gas went into 2 places, the body of the stove and losses from the outside. The heat loss into the stove body is calculated by summing the temperatures of all 10 nodes at the end of the cooking event, and multiplying by appropriate masses and by the specific heat. The heat lost from the outside was obtained by numerically integrating the convective and radiative heat loss rates. Time steps were 1 second, which is typically less than 1/10 that required for numerical stability. Calculations were done using EES (Engineering Equation Solver) software available from F-Chart Software. For reference, the complete code is given in Appendix 3.

In generating the maps, the following assumptions were made. The specific heat was assumed to be 835 J/kg-C, and the material thickness was assumed to be 3 cm. The specific heats of various stove materials vary over a narrow range, and the assumed value should be acceptable in any calculations. As stated previously, over a wide range of values, the total heat loss is not highly dependent on the material thickness. The thermal conductivity was assumed to be constant at the room temperature value. At stated previously, for the lightweight materials one might add about 10% to the calculated heat loss to account for this effect.

Appendix 3: Full listing of computer code

Below is a full listing of the computer code used to generate these results. Statements are included for both the constant thermal conductivity calculations and the variable thermal conductivity calculations.

procedure solve(k:totalqlost,hoeff,qout,qbody)
{comments are in brackets}

deltat=1
tend=3600
c=835
rho=770
L=.03
deltal=l/9 {10 nodes}
alpha=k/(rho*c)
deltatmax=.5*deltal^2/alpha {maximum allowable delta t for numerical stability}
m=rho*deltal
T=700 {degrees C, internal temp minus ambient temp}
area=.1178
t[1]=T
duplicate j=2,10
t[j]=0
end

time=0
qout=0

repeat {start loop}

time=time+deltat

duplicate i=2,9
t[i]=t[i]+deltat*k*(1+t[i]*1.8/2220)/deltal*((t[i-1]-2*t[i])+t[i+1])/(m*c) {use this expression for variable thermal conductivity}
{t[i]=t[i]+deltat*k*(1)/deltal*((t[i-1]-2*t[i])+t[i+1])/(m*c)} {use this expression for constant thermal conductivity}
end

ho=1.7*t[10]^.25 {convective heat loss coefficient}
qlostconv=ho*t[10] {W/m^2}
qlostrad=5.67e-8*((t[10]+20+273)^4-293^4) {W/m^2}
t[10]=t[10]+deltat/(m*c/2)*(k*(1+t[9]*1.8/2220)/deltal*(t[9]-t[10])-qlostconv-qlostrad) {use this expression for variable thermal conductivity}
{t[10]=t[10]+deltat/(m*c/2)*(k*(1)/deltal*(t[9]-t[10])-qlostconv-qlostrad)} {use this expression for constant thermal conductivity}

qout=qout+area*deltat*(qlostconv+qlostrad)
hoeff=(qlostconv+qlostrad)/t[10]

until (time>=tend) {end loop}

qbody=area*m*c*(t[2]+t[3]+t[4]+t[5]+t[6]+t[7]+t[8]+t[9]+t[1]/2+t[10]/2)
totalqlost=qout+qbody

end {end of procedure}

k=.107
call solve(k:totalqlost,hoeff,qout,qbody)
lossfactor=totalqlost/700/.1178

jordan Release Dates